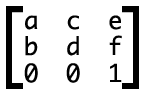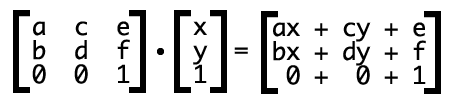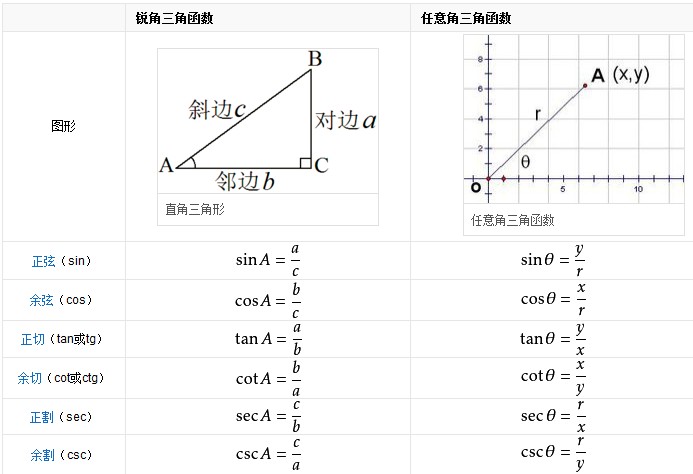
大学没好好学习高数线性代数，工作中遇到麻烦了，从大师那里 文章 学习一下矩阵。 先是复习下三角函数，sin cos tan 总是记不住。

CSS3中的矩阵

CSS3中的矩阵式一个方法，matrix() 和 matrix3d() 前者为2D平面的移动变换(transform), 后者是3D变换，2D变换矩阵为33，3D变换矩阵为44。今天只学习2D变换。 transform有斜拉(skew),缩放(scale)，旋转(rotate)以及位移(translate)，这些方法的实现其实都是使用matrix几个固定值实现，理解matrix可以更好的理解这些转换，还可以实现一些更复杂的变换。

transform 与坐标系统

transform旋转默认是围着中心旋转的，而这个中心点是 transform-origin属性对应的点，也是矩阵计算的一个重要依据点。

transform matrix 与偏移

CSS3 transform 的matrix() 方法写法如下：

transform: matrix(a, b, c, d, e, f)

这6个参数对应的矩阵是下图，注意书写方向是竖着的。

而矩阵计算则是

其中x,y表示转换元素的所有坐标（变量），转换时会对每一个像素进行矩阵计算。

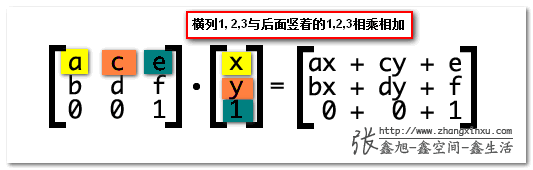
矩阵的乘法，33矩阵每一行的第1个值与后面13的第1个值相乘，第2个值与第2个相乘，第3个与第3个，然后相加，如下图同色标注：

ax+cy+e即为变换后的水平坐标， bx+dy+f表示变换后的垂直位置。

举例

transform: matrix(1,0,0,1,30,30)

经过计算，(0,0)位置转换为了30,30 ax+cy+e = 1*0+0*0+30 = 30 , bx+dy+f = 0*0 + 1*0 +30 = 30

实际上 transform: matrix(1,0,0,1,30,30) 就是 transform: translate(30px, 30px) 注意 translate需要单位，而matrix的e,f参数可以省略单位。

transform: matrix(与我无关, 哪位, 怎么不去高考, 打麻将去吧, 水平偏移距离, 垂直偏移距离);

transform matrix矩阵与缩放，旋转以及拉伸

缩放(scale)

观察上边的matrix(1, 0, 0, 1, 30, 30);偏移后比例没有变化，而参数中有两个1，这两个1中的第一个缩放 x轴， 第二个缩放y轴。 假设比例是s，矩阵是 matrix(s, 0, 0, s, 0, 0);套用公式就是

x' = ax + cy + e = sx + 0y + 0 = sx;
y' = bx + dy + f = 0x + sy + 0 = sy;

也就是matrix(sx, 0, 0, sy, 0, 0); 等同于 scale(sx, sy);

旋转(rotato)

方法和参数如下(假设角度为0)

matrix(cos0,sin0,-sin0,cos0,0,0)

结合矩阵公式，就有：

x' = x*cos0 - y*sin0 + 0 = x*cos0 - y*sin0
y' = x*sin0 + y*cos0 + 0 = x*sin0 + y*cos0

四个参数可以记忆为 CS-SC : 初三 - 上床

旋转30deg transform:rotato(30deg) 等同于 transform:(0.866025, 0.5, -0.5, 0.866025, 0, 0) 虽然很复杂，但是可以在看到前四位参数都有值时判断为旋转

拉伸 (skew)

拉伸是和bc参数有关系，书写一下（y轴倾斜角度在前）:

matrix(1, tan(0y), tan(0x), 1, 0, 0)

套用矩阵公式计算为

x' = x+y*tan(θx)+0 = x+y*tan(θx) 
y' = x*tan(θy)+y+0 = x*tan(θy)+y

###使用matrix实现复杂效果， 在他的网站上有一个例子 地址